---【追記:2022-04-01】---
「基礎線形代数講座」のPDFファイルをこの記事から直接閲覧、ダウンロードできるようにしました。記事内後半の「公開先」に追記してあります。
--- 【追記ここまで】---
みなさん、はじめまして。技術本部 開発技術部のYです。
ひさびさの技術ブログ記事ですが、タイトルからお察しの通り、今回は数学のお話です。
#数学かよ って思った方、ごめんなさい(苦笑)
数学の勉強会
弊社では昨年、有志による隔週での数学の勉強会を行いました。ご多分に漏れず、コロナ禍の影響で会議室に集合しての勉強会は中断、再開の目処も立たず諸々の事情により残念ながら中止となり、用意した資料の配布および各自の自学ということになりました。
勉強会の内容は、高校数学の超駆け足での復習から始めて、主に大学初年度で学ぶ線形代数の基礎の学び直し 、および応用としての3次元回転の表現の基礎の理解といった感じです。
「線形代数」とは、微積分と並び理工系の科学・技術の諸分野で基礎中の基礎として用いられる数学の分野で、ゲームでは主に3DCGの技術的基礎として応用されています。昨今のAIブームでも一時期話題になりました。 タイトルにある「クォータニオン」とは、日本語では「四元数」と訳され、ゲームではキャラや背景などを3次元回転させるときに応用されるもので、勉強会の中では最後に出てくるラスボスであり少し難しい数学の概念です。
勉強会の趣旨は、この「クォータニオン」を数学的にきちんと理解することを えさ ゴールとして、そのために(実際はそれだけでなくさまざまな技術の基礎となっている)「線形代数」の基礎をきちんと学び直そうということでした。
なぜ数学?
ゲーム開発においても分業化・専業化の流れは著しく、ゲームアプリケーション(みなさんに遊んで頂いているゲームそのもの)を開発する際、いわゆるゲームエンジンや各種ライブラリを用いるのが当たり前になっています。これらエンジンやライブラリは、ゲーム開発者にさまざまな機能を提供し効率よく開発できるようにすることが役割であり、極端な話、三角関数を全く知らなくても3Dゲームを作れる時代になっています。 しかしながら例えばゲーム固有の表現のためにシェーダー(画面を描画する機能)をカスタマイズしたい場合や、当然のことながらエンジンやライブラリそのものの開発者は、ある程度のさまざまな数学の知識が必要となります。技術的に高度なことをしようと思うとなおさら深い理解が必要です。
このように数学や物理学は、ゲーム業界のみならず理工系のさまざまな分野で、科学者・技術者を根元から支える基礎となり重要な武器となっています。
資料を公開します
今回、この勉強会用に用意した資料「基礎線形代数講座:線形代数 回転の表現」を一般に公開いたします。全8講、本文が全部で140ページのPDFで、各講は以下のような標題です。
- 第1講 イントロダクション
- 第2講 初等関数
- 第3講 ベクトル
- 第4講 行列 I:連立一次方程式
- 第5講 行列 II:線形変換
- 第6講 行列 III:固有値・対角化
- 第7講 回転の表現 I
- 第8講 回転の表現 II
線形代数 基礎の本質的な部分をできるだけ簡潔に分かりやすく学べるように全体を組み立ててみました。各項目を学ぶ順番や手法、一部は定義すら一般的なものと違う(例:行列式)こともあります 。いわゆる「大人の学び直し」ではあるのですが、内容はガチの数学となっています。 記事の最後に公開先へのリンクを張っておきますので、興味のある方は参考にして頂ければと思います。
特に学生の方で、この資料で線形代数を学んでみようと思われた奇特な方がいらっしゃれば、言うまでもないことですが読んだ後改めて講義で指定されている教科書を読んでみましょう。きっとこれまで以上に理解が深まることと思います。
この記事では、その中から「クォータニオン」の導入部分である、第8講の第2節までをそのまま引用します。導入部なので内容は平易となっていますが、複素数・行列・三角関数に関するある程度の知識がないと理解は難しいと思われます。ぜひ紙と鉛筆を用意して、ご自身でも図や式を書いたり計算したりしながら、じっくり読んでみてください。
基礎線形代数講座からの引用
【8-1】はじめに
本講では、4種の3次元回転の表現の最後としてクォータニオンについて学ぶ。クォータニオンは日本語では四元数(しげんすう)と訳されるもので、1843年にハミルトンにより発見された複素数を拡張した代数体系であり、3次元の回転の表現としても多くの利点を備えている。
その性質から特に計算機を用いる場合にも他の表現手法に比べ優位な点が多く、近年 宇宙機を始め、3DCGやCV、ロボット工学等々さまざまな分野で応用されている。一方で他の表現手法に比べるとやや抽象的でその本質(4次元空間に埋め込まれた3次元回転)が捉えづらい面も否めない。本講では、拡張の元になった大きさ1の複素数の積による複素平面内での回転の復習から始め、ハミルトンによる発見に至るまでの過程*1をたどる事でクォータニオンを導入し、その性質を分かりやすく解説する。
●おさらい
任意の複素数 $ x+iy $ に大きさ $ 1 $ の複素数 $ \cos\theta+i \sin\theta $ を掛ける事は複素平面内での $ \theta $ 回転を表していた。実際
\[
(x'+iy')=(\cos\theta+i\sin\theta)(x+iy)=(x\cos\theta-y\sin\theta)+i(x\sin\theta+y\cos\theta )
\]
この式で、$ 1 $ と $ i $ をベクトルの基底としてみると、
\[
x→x'=x\cos\theta-y\sin\theta,\ y→y'=x\sin\theta+y\cos\theta
\]
という線形変換と見ることができて、行列形式で書けば
\[
\begin{eqnarray}
\left[
\begin{array}{c}
x' \\
y' \\
\end{array}
\right]=\left[
\begin{array}{cc}
\cos\theta & -\sin\theta\\
\sin\theta & \cos\theta\\
\end{array}
\right] \left[
\begin{array}{c}
x \\
y \\
\end{array}
\right]
\end{eqnarray}
\]
となり、すなわち複素平面である $ 1-i $ 平面での $ \theta $ 回転を表している事がわかる。
これの本質は、$ i $を掛けるという事:基底 1 と $ i $ との閉じた代数が、$ 1-i $ 平面内で一回りする回転に相当していることにある。

【8-2】クォータニオンの導入:ハミルトン劇場
[8-2-1] 拡張複素数で複素( 3次元)空間を回したい
ハミルトンは複素数を拡張して、虚数単位 $ i $ の他に独立な別の虚数単位 $ j $ を導入
$( i^2=-1,\ j^2=-1,\ \overline {i}=-i,\ \overline {j}=-j)$、$ 1,i,j $ の 3つの元で $ 1-i $平面、$ 1-j $平面、$ i-j $平面それぞれの回転を表現できないか?と考えた(つまり複素平面を複素空間に拡張できないか?ってこと) 。

「独立な異なる虚数単位 $ i,j $」に違和感がある人もいると思う。新しい代数として拡張していっているので、うまく拡張できさえすればあとは「慣れ」ではあるのだが「複素数」を以下のように解釈することで別の虚数単位を導入するという拡張も違和感が減るかもしれない。
おさらい*2:2行 2列の行列
$
\begin{eqnarray}
I= \left[
\begin{array}{cc}
0 & -1\\
1 & 0\\
\end{array}
\right]
\end{eqnarray}
$ を考えると(この行列は 上の おさらいで出てきた 2次の
回転行列で $ \theta=\pi/2 $ としたものでもあることに注意)、
$
\begin{eqnarray}
I^2= \left[
\begin{array}{cc}
-1 & 0\\
0 & -1\\
\end{array}
\right] = -E
\end{eqnarray}
$
( $ E $ は単位行列 )となる(つまり 2乗して -1)。また行列 $ Z=xE+yI\ (x,y∈\Bbb R ) $ を考えると、
$
\begin{eqnarray}
Z = \left[
\begin{array}{cc}
x & -y\\
y & x\\
\end{array}
\right]
\end{eqnarray}
$
なので、$ Z = O $ となるのは $ x=y=0 $ のときのみ(つまり $ E $ と $ I $ は線形独立)。この行列 $ Z=xE+yI $ に対し $ E $ を $ 1, I $ を $ i $ に対応させることで、複素数 $ z=x+iy $ に対応させる事が可能となる。
ここでさらに別の行列 例えば
$
\begin{eqnarray}
J = \left[
\begin{array}{cc}
1 & -\sqrt{2}\\
\sqrt{2} & -1\\
\end{array}
\right]
\end{eqnarray}
$
を考えると、$ J^2=-E $ を満たし、この $ J $ を含め $ E,I,J $ が線形独立であることは容易に確かめられる。このような「複素数の拡張」(上の $ J $ の事)がうまく行くかどうかは別にして「違和感」のない表現もやろうと思えば可能ではある。
以下、ハミルトンがクォータニオンを発見するまでの過程*3をたどってみよう。
ハミルトン:$ 1-i $平面と $ 1-j $平面の回転は当然できた。

でも $ i-j $平面がうまくいかない。 $ i\times j $ の扱いがどうにもこうにも…
とりあえず $ i\times j $ を $ ij $ として回るようにはできたけど*4、この $ ij $ って本来 $ i $ にならないと $ i-j $平面にはならない。でも $ ij = i $ としてしまうと $ i $ を掛けても $ -j $ にならずに $ -1 $ となってうまく回らない。どうしたものか・・・
(ちなみに後に別の数学者により、このような $ 1,i,j $ による 「複素数の拡張」(三元数に相当)は、うまく行かない事が証明されている。)
[8-2-2] 4次元? マジか 4次元??
ある日運河のほとりを歩いている時(実話*5)にひらめいた: もう一つ虚数単位を導入して $ i\times j=k $ としてみよう。実数単位 $ 1 $ と虚数単位 $ i,j,k $ で 4次元になるけど、うまくいくかも・・・
回転面は $ 1-i, 1-j, 1-k $平面, $ i-j, j-k, k-i $平面の6面になるのか。3次元回転をうまく取り出すには、$ i-j, j-k, k-i $平面の回転がこんな風になるといいのかな?
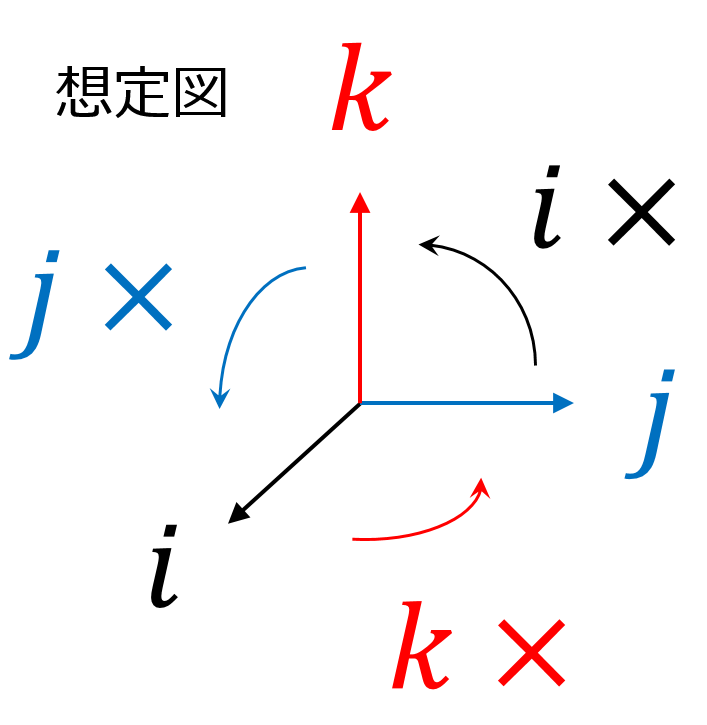
●$ i $ を掛けると?:想定図のように $ j-k $平面を回すため、$ ij=k $ としてみよう

お、$ j-k $平面だけでなく $ 1-i $平面も同時に回るんだ。そりゃそうか。しかもそれぞれの平面内で回りそうだ。
角度 $ \theta $ の場合として「大きさ」1の $ (\cos \theta+ i \sin \theta) $ を、4次元に拡張した「複素数」$ (w+ix+jy+kz) $ に( $ i^2=-1,\ ij=k, \ ik=-j $ に注意して)掛けてみよう:
\[
\eqalign{
(w'+ix'+jy'+kz')=(\cos\theta&+i\sin\theta)(w+ix+jy+kz)\\
=&w\cos\theta+ix\cos\theta+jy\cos\theta+kz\cos\theta\\
&+iw\sin\theta-x\sin\theta+ky\sin\theta-jz\sin\theta\\
=&(w\cos\theta-x\sin\theta)+i(w\sin\theta+x\cos\theta)\\
&+j(y\cos\theta-z\sin\theta)+k(y\sin\theta+z\cos\theta) \tag{8-2-1}\\
}
\]
確かに $ w-x $平面( $ 1-i $平面:下から2行目)と $ y-z $平面( $ j-k $平面:下から1行目)がそれぞれの平面内
で同時に別々に回っている*6。
| つまりこういうこと |
|---|
| \begin{eqnarray} \left[ \begin{array}{c} w' \\ x' \\ y' \\ z' \\ \end{array} \right]=\left[ \begin{array}{cccc} \cos\theta & -\sin\theta & 0 & 0\\ \sin\theta & \cos\theta & 0 & 0\\ 0 & 0 & \cos\theta & -\sin\theta\\ 0 & 0 & \sin\theta & \cos\theta\\ \end{array} \right] \left[ \begin{array}{c} w \\ x \\ y \\ z \\ \end{array} \right] \end{eqnarray} |
●$ j $ を掛けると?:想定図のように $ k-i $平面を回すため、$ jk=i $ としてみよう

およ。さっきの $ i $ を掛けて $ j-k $平面をうまく回せる条件:$ i\times j=k $ と合わせると、$ ij=k,\ ji=-k $ となって、なんと積は可換じゃなくなる! まあしょうがないか…。
角度 $\theta$ だと同様に:
\[
\eqalign{
(\cos\theta&+j\sin\theta)(w+ix+jy+kz)\\
=&(w\cos\theta-y\sin\theta)+j(w\sin\theta+y\cos\theta)\\
&+k(z\cos\theta-x\sin\theta)+i(z\sin\theta+x\cos\theta) \tag{8-2-2}\\
}
\]
ん、これも別々に回っている。
●残り $ k $ を掛けると?:想定図のように $ i-j $平面を回すため、$ ki=j $ としてみよう

これも角度 $\theta$ だと同様に:
\[
\eqalign{
(\cos\theta&+k\sin\theta)(w+ix+jy+kz)\\
=&(w\cos\theta-z\sin\theta)+k(w\sin\theta+z\cos\theta)\\
&+i(x\cos\theta-y\sin\theta)+j(x\sin\theta+y\cos\theta) \tag{8-2-3}\\
}
\]
●とりあえず分かったこと
虚数単位 $ i,j,k $ に対して積を $ ij=k, ji=-k, jk=i, kj=-i, ki=j, ik=-j $ として $ w+ix+jy+kz $ に左から $ \cos\theta+i\sin\theta $ を掛けると、$ 1-i $平面, $ j-k$平面が同時に $ \theta $ 回転 する。$ j,k $ で回しても同様。でもこのままだと$ 1-i $平面で余計な回転が発生し、最終的に実現したい純粋な 3次元の回転を切り出せない。何かうまい方法はないのだろうか?
| つまりこうなって欲しい |
|---|
| \begin{eqnarray} \left[ \begin{array}{c} w' \\ x' \\ y' \\ z' \\ \end{array} \right]=\left[ \begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & \cos\theta & -\sin\theta\\ 0 & 0 & \sin\theta & \cos\theta\\ \end{array} \right] \left[ \begin{array}{c} w \\ x \\ y \\ z \\ \end{array} \right] \end{eqnarray} |
●そういえば非可換だった*7
非可換なので、右から掛けたらどうなる?
右から $ i $ を掛けた場合:

なんと $ 1-i $平面は同じ向きで、$ j-k $平面は逆向きに回る!じゃあ $ -i $ だとその逆になるだろう。
右から $ -i $ を掛けた場合:

これなら、左から $ i $ を、右から $ (-i) $ を掛けることで $ 1-i $平面の回転だけを無くせそう。
●というわけで
左から $ i $ 右から $ -i $ を掛けた場合:

$ j-k $平面は2倍回りそうだけどw やってみよう。
\[
\eqalign{
(\cos\theta&+i\sin\theta)(w+ix+jy+kz)(\cos\theta-i\sin\theta)\\
=&(\cos\theta+i\sin\theta)\{(w\cos\theta+x\sin\theta)+i(-w\sin\theta+x\cos\theta)\\
&+j(y\cos\theta-z\sin\theta)+k(y\sin\theta+z\cos\theta)\}\\
=&w\cos^2\theta+x\sin\theta\cos\theta-(-w\sin^2\theta+x\sin\theta\cos\theta)\\
&+i(-w\sin\theta\cos\theta+x\cos^2\theta)+j(y\cos^2\theta-z\sin\theta\cos\theta)\\
&+k(y\sin\theta\cos\theta+z\cos^2\theta)+i(w\sin\theta\cos\theta+x\sin^2\theta)\\
&+k(y\sin\theta\cos\theta-z\sin^2\theta)-j(y\sin^2\theta+z\sin\theta\cos\theta)\\
=&w(\cos^2\theta+\sin^2\theta)+ix(\cos^2\theta+\sin^2\theta)\\
&+j\{y(\cos^2\theta-\sin^2\theta)-z(2\sin\theta\cos\theta)\}\\
&+k\{y(2\sin\theta\cos\theta)+z(\cos^2\theta-\sin^2\theta)\}\\
=&w+ix+j(y\cos2\theta-z\sin2\theta)+k(y\sin2\theta+z\cos2\theta)\tag{8-2-4}
}
\]
最後は倍角の公式を使った。これで $ j-k $平面 だけを回せた!
めでたしめでたし。2倍回るけどw
| こうなった |
|---|
| \begin{eqnarray} \left[ \begin{array}{c} w' \\ x' \\ y' \\ z' \\ \end{array} \right]=\left[ \begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & \cos2\theta & -\sin2\theta\\ 0 & 0 & \sin2\theta & \cos2\theta\\ \end{array} \right] \left[ \begin{array}{c} w \\ x \\ y \\ z \\ \end{array} \right] \end{eqnarray} |
・・・ハミルトン劇場 終
このあと第8講は
- 【8-3】クォータニオン:定義と諸性質
- 【8-4】クォータニオン:3次元回転の表現
- 【8-5】 [▼]付録 1:一般的な4次元の回転について
- 【8-6】付録2:成分表示における4次元内積の不変性について
- 【8-7】 [▼A]付録 3:オイラーの公式と代数的補間式 について
と続きます・・・。
公開先
--- 【追記:2022-04-01】 ---
PDFファイルは以下のリンク先でも閲覧、ダウンロードできます。

--- 【追記ここまで】 ---
--- 【更新:2022-07-15】---
「基礎線形代数講座」は、開発技術部の技術資料一般公開先でもある、Speaker Deck サイトにて公開しています。
#技術資料一般公開先サイトを Speaker Deck に引っ越しました
--- 【更新ここまで】 ---
--- 各項目は以下のような内容となっています。
【第1講】イントロダクション
【1-1】はじめに
【1-2】数学導入:数の拡張
[1-2-1] 自然数 ℕ:全てはここから
[1-2-2] 整数 ℤ:0の発見、負の数の導入
[1-2-3] 有理数 ℚ :分数・小数の導入
[1-2-4] 実数 ℝ:無理数の導入
[1-2-5] 複素数 ℂ:虚数の導入
[1-2-6] まとめ
【1-3】付録:ギリシャ文字一覧
【第2講】初等関数
【2-1】はじめに
【2-2】指数・対数関数
[2-2-1] 指数関数の定義と性質
[2-2-2] 対数関数の定義と性質
[2-2-3] 自然対数と自然指数
[2-2-4] 応用例
【2-3】三角関数
[2-3-1] 三角関数の定義と性質
[2-3-2] 三角関数の主な公式
[2-3-3] ド・モアブルの定理
[2-3-4] 応用例
【2-4】指数関数の別定義
【2-5】[▼A] オイラーの公式
【2-6】付録1:二項定理(二項展開)
【2-7】付録2:総和記号
【2-8】付録3:sinθ/θ→ 1 (θ→ 0) の証明
【2-9】付録4:三角関数の各公式の証明
【第3講】ベクトル
【3-1】はじめに
【3-2】ベクトルがもつ性質
[3-2-1] ベクトル自体がもつ性質
[3-2-2] ベクトルの組がもつ性質
【3-3】内積
[3-3-1] 定義
[3-3-2] 代数的性質
[3-3-3] 幾何学的意味
【3-4】抽象化されたベクトルの概念と例
【3-5】外積
[3-5-1] 定義
[3-5-2] 代数的性質
[3-5-3] 幾何学的意味
【3-6】n本のベクトルが張るn次元体積
[3-6-1] 2次元:2次元体積(面積)
[3-6-2] 3次元:3次元体積(体積)
[3-6-3] n次元:n次元体積
【3-7】付録1:Levi-Civita記号
[3-7-1] Levi-Civita記号 (3次の場合)
[3-7-2] 拡張Levi-Civita記号 (n次の場合)
【3-8】付録2:外積の公式の証明
【3-9】付録3:置換と転倒数の偶奇性
【第4講】行列I:連立一次方程式
【4-1】はじめに
【4-2】掃き出し法
[4-2-1] 連立一次方程式の加減法による解法
[4-2-2] 掃き出し法と行基本変形
[4-2-3] 不定解、解なしとなる場合
[4-2-4] 連立一次方程式の違う見かた
【4-3】行列式の導入
[4-3-1] あらためて「関数」D(a,b,c) とは
[4-3-2] 行列式の定義
[4-3-3] 行列式の性質 I
【4-4】行列の導入
[4-3-1] 導入小話:もしかすると行列って・・・・
[4-4-2] 行列と演算の定義
[4-4-3] 行列の基本性質
[4-4-4] 連立一次方程式の行列による表示
【4-5】付録1:行列式の重要な性質
【4-6】付録2:簡約行列の構造
【4-7】付録3:補足説明
【4-8】付録4:行列式の定義について
【第5講】行列II:線形変換
【5-1】はじめに
【5-2】線形変換(一次変換)
[5-2-1] 線形変換の例
【5-3】逆行列
[5-3-1] 行列式の性質II:余因子展開と積の行列式
[5-3-2] 逆行列の定義と余因子行列による表示
[5-3-3] 正則行列/逆行列の性質
【5-4】直交行列
[5-4-1] 転置行列の性質
[5-4-2] 直交行列の定義と性質
【5-5】線形変換の行列による表示
[5-5-1] この節のねらい
[5-5-2] 必要な諸定義
[5-5-2] ベクトルの列ベクトルによる表示
[5-5-3] ベクトルの組の行列による表示
[5-5-4] 線形変換の行列による表示
[5-5-5] 基底の変換と座標変換
[5-5-6] 線形変換に対する基底の変換と表示行列の変換
[5-5-7] 線形変換と座標変換(ActiveとPassive)
[5-5-8] 合成変換の行列による表示
【5-6】[▼C]付録1:Levi-Civita記号の積の性質
【5-7】付録2:複素数の行列による表現
【第6講】行列III:固有値・対角化
【6-1】はじめに
【6-2】固有ベクトルと固有値
[6-2-1] 線形変換の点の「向きの流れ」
[6-2-2] 固有ベクトル・固有値と固有方程式
【6-3】行列の対角化
[6-3-1] 線形独立な固有ベクトルへの基底の変換
[6-3-2] 対角化可能な条件
[6-3-3] 相似変換
[6-3-4] 行列の三角化
[6-3-5] 固有値の諸性質
【6-4】実対称行列の対角化
[6-4-1] 実対称行列の固有値・固有ベクトル
[6-4-2] グラム・シュミットの正規直交化法
[6-4-3] 実対称行列の対角化
[6-4-4] 実二次形式
【6-5】応用例
[6-5-1] 剛体回転におけるオイラーの定理
[6-5-2] 漸化式と特性方程式
[6-5-3] [▼B] フーリエ級数展開
[6-5-4] 行列指数関数
【6-6】付録1:複素ベクトル空間・行列について
【6-7】付録2:各証明
【6-8】[▼A]付録3:オイラーの公式の行列表現
【第7講】回転の表現I
【7-1】はじめに
【7-2】回転行列
[7-2-1] 考察の定式化
[7-2-2] 表示行列としての回転行列
【7-3】オイラー角と仲間たち
[7-3-1] 回転後の基底の姿勢を3つの回転角で表す
[7-3-2] オイラー角
[7-3-3] Tait-Bryan角
[7-3-4] ジンバルロック
【7-4】回転ベクトル
[7-4-1] 定義とロドリゲスの回転公式
[7-4-2] 回転行列による表示
[7-4-3] 回転行列の固有値・固有ベクトル
[7-4-4] 3次元回転の大域的な構造
【7-5】付録1:回転変換に関する2証明
【7-6】[▼A,C]付録2:3次回転行列となる行列指数関数
【第8講】回転の表現II
【8-1】はじめに
【8-2】クォータニオンの導入:ハミルトン劇場
[8-2-1] 拡張複素数で複素(3次元)空間を回したい
[8-2-2] 4次元? マジか4次元??
【8-3】クォータニオン:定義と諸性質
[8-3-1] 定義
[8-3-2] スカラー+ベクトル表記
[8-3-3] ベクトル部の性質
[8-3-4] ノルム・逆元と積の性質
[8-3-5] 単位クォータニオンと極形式
[8-3-6] 4次元ベクトルとしての内積
【8-4】クォータニオン:3次元回転の表現
[8-4-1] 任意軸まわりの回転
[8-4-2] 3次元回転の合成
[8-4-3] 回転行列による表示
[8-4-4] 単位クォータニオンのパラメータ領域
[8-4-5] 球面線形補間
【8-5】[▼]付録1:一般的な4次元の回転について
【8-6】付録2:成分表示における4次元内積の不変性について
【8-7】[▼A]付録3:オイラーの公式と代数的補間式について
---
セガでは共に技術力を高め合い研鑽していける方を募集しています。 興味がある方は下記サイトにアクセスして下さい。
*1:あくまで筆者の想像(妄想)による過程であり、史実に基づいたものではありません。
*2:詳細は第5講 付録2参照
*3:くどいですが、筆者による想像(妄想)です
*4: $ 𝑖\times 𝑖𝑗=𝑖^2𝑗=−𝑗 $ ってこと
*5:運河を渡る橋に $ 𝑖^2=𝑗^2=𝑘^2=𝑖𝑗𝑘=−1 $ と刻んだとの事
*6:ちなみに 4次元では 2本の直交する基底で張られる (回転 )面を、基底を共有せずに 2面とることが できる( 3次元ではできない)。この場合 $ 1−𝑖 $平面 と $ 𝑗−𝑘 $平面 は原点のみで交わっている事に注意。
*7:ハミルトン卿ご自身は、この積の非可換性(当時初?)あまりお気に召さなかったらしい
