Inverse Kinematics(IK)について

SEGA ゲーム プログラマー Animation エンジニア 数学

はじめに

株式会社セガ 第3事業部 オンライン研究開発プログラム2部の松本と申します。

今回はInverse Kinematics(IK)に関する基本的な考え方や手法についての記事となります。

ゲーム制作の仕事に携わっているとIKの名前くらいは聞いたことがあるのではないかと思いますが、実際の中身については何をやってるのか良く分からない謎の技術だと感じている人も多いのではないでしょうか。この記事を読んでInverse Kinematicsについての理解を深めたり、あるいは改めて学び直すための良い機会になればと思います。

特にゲーム制作者ではない方にとっては、前提知識が不足していて分かり辛い所もあるかも知れませんが、本題であるIKそのものの概念や処理内容については、高校数学課程の知識 *1 があれば十分に理解できそうな内容になっているので、そうした視点で数学の復習がてら読んでみるのも良いかと思います。SNS等で度々話題になるベクトルや三角関数と言った高校数学で習う項目の有用性を感じてもらうだけでも構いません。

目次

IKの正体

まずはIKというのがどういう物なのかを説明したいのですが、いくつか前提となる知識も必要となるので、そちらから順番に説明します。

FKについて

人体のように複数の関節が連なって構成される骨格構造の姿勢を決定していく際に、構造の開始位置となるルート(=根っこ)関節から始めて、構造の終端側にある関節に向かって順番に平行移動や回転変換による姿勢計算を繰り返すことで、全身の姿勢を決定していく手法が考えられます。

この様な逐次的な手順で多関節連鎖構造の姿勢を解決する手法を、Forward Kinematics(フォワード・キネマティクス=順運動学)と呼びます。長いので今後はFK(エフ・ケー)と省略します。

FKによる平行移動と回転のイメージ図

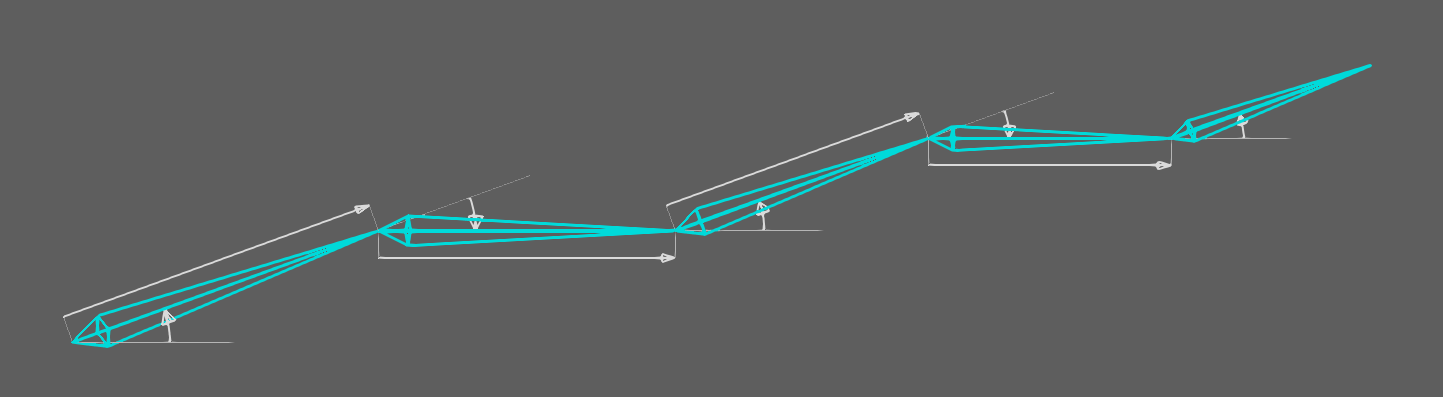
FKの役割

ゲームに登場する3Dキャラクターの動きは、あらかじめ用意されているモーションデータを再生することで表現されていることがほとんどですが、この処理はFKによって計算されています。つまりFKはモーション再生処理に欠かせない基盤技術という位置付けです。

実際のFKモーションデータの大半は回転データの塊ですが、適切な全身のポーズや動きを作るために、どの関節にどのくらいの回転量を与えるのがいいのかというのは、FKでは決めることができません。計算で決めることができないのはもちろんのこと、人の手を使ったとしてもFK的な手続きによるデータ作成は、極めて非効率的な作業となります。ここで言うFK的手続きというのは、関節の回転角を1つずつ編集することで目的の全身ポーズや動作をつくることを指します。例えば関節が動くフィギュアやプラモで全身のポーズを付ける作業手順が、おおよそこれに該当するので、経験したことのある方は、あの作業で複雑で細かい動きを作るのがどれだけ大変か想像がつくのではないでしょうか？

まとめると、FKは既に決まっている回転データを順番に処理して姿勢を作り上げるという基礎的な役割を担いますが、その回転量そのものを決めることができないため、モーションデータを作成するだけでなく、ゲーム中にモーションの再生結果を加工して別の動きを作り出すのも難しい、ということになります。

ようやくIKの登場

そこで、制御し易い情報を与えることで、FK処理に必要な回転量を決めるための機能が求められます。

特定の部位の位置や姿勢を指定することで、そこに到達するまでの中間の関節の姿勢(=回転量)を全て計算で決める手法、すなわちInverse Kinematics(インバース・キネマティクス=逆運動学)と呼ばれる手法が、その役割を担います。こちらも今後はIK(アイ・ケー)と略します。

IKには様々な手法があり、その手法や適用範囲にも寄りますが、例えば手先の位置を決めたら、そこに連結されている前腕や上腕、場合によっては肩や背骨、そこに連結された反対側の腕の姿勢までも一度に決めるようなことも可能です。これはモーションデータを作る際にも非常に効率的なので、モーションデザイナーが扱うツールには必須の機能となっていますし、ゲーム中で再生されたモーションの結果をゲーム側の都合に合わせて修正・加工したりするのにも使われています。

IKは難しい？

計算でどのように回転量を決めるのかはパッとは思いつかないかも知れませんが、具体的なIKの手法そのものは、知ってしまえば超簡単な物から、理論背景を理解するだけでも難しい物まで様々です。今回紹介するのは基本的なアルゴリズムで、仕組みや理論は比較的簡単な部類に入るものですが、手法そのものの実用性や重要性は非常に高く、今でも多くのゲームで使われているので、学びのコストパフォーマンスはかなり良いはずです。

1ボーンIK

概要

多関節の連鎖で構成される骨格構造を1つ1つ分解すると、1つの関節とそれに対応する骨(ボーン)に相当する部位に分解できます。この単体骨に適用するIKが1ボーンIKです。1ボーンIKを組み合わせて多関節のNボーンIKとすることはできませんが、2ボーン以上のIK処理の多くが内部処理に利用している重要なIKです。

下の図は1ボーンIKの動作概要を示した図です。このような図は今後も出てくるので、その見方と合わせて動作概要を説明します。

1ボーンIKの概念図

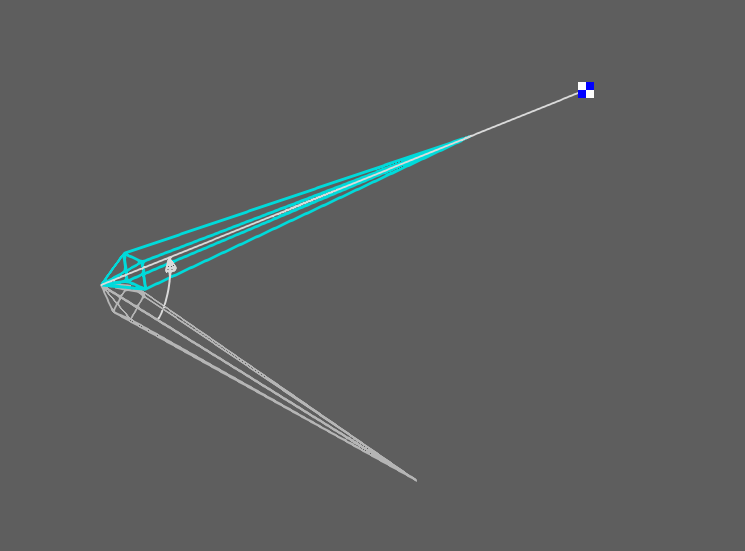
図には、ちょっと太めの針のようなモデル表示が灰色と水色で2本分描かれています。これが制御対象の骨の初期配置(灰色)と、1ボーンIK適用後の配置(水色)を表しています。針の尖った方向がこの骨の進行方向になり、針の根本から先端までの長さはそのまま骨の長さを表します。水色の針モデルの延長線上にある白と青の四角いチェッカーマークがありますが、その中心がIKの目標位置を表しています。この図は1ボーンIKを適用したことで、骨の進行方向が目標位置の方向を向いているということを表したものです。

このように、1ボーンIKが達成する処理内容は、ある目標位置が1点与えられたら、骨の進行方向をその点の方向に向けるというものになります。IKは一般的には、与えられた目標位置に骨の先端位置が到達するような姿勢を解として導き出しますが、1ボーンの場合はそれを達成できるのが、目標位置が骨の長さと同じ距離にある場合だけなので、進行方向が合えばOKとしています。

骨の進行方向を目標位置に向けるというのは、単純に関節の位置から目標位置に向けたベクトルを計算して、骨の長さに合わせれば完了という訳にはいきません。骨の進行方向に関してはそれで解決するのですが、関節の姿勢がどのように変化したかは、それだけでは不十分だからです。

具体的な手法の説明に移る前に、少しだけ関節の姿勢について説明します。

前提知識1：X軸Y軸Z軸による姿勢表現について

各関節の姿勢は、それぞれのX軸、Y軸、Z軸の方向で与えることができます。CGなどの分野では、関節の進行方向をX軸に割り当てるのが主流となっているので、ここでもそれを前提に説明します。
先ほどのベクトル計算では、このX軸の方向を向けることはできていますが、Y軸、Z軸に関しては未解決です。X軸を回転させたのと同じ分だけY軸やZ軸も回転させることで、初めて関節の方向が変わったことになります。

3次元の場合はXYZ全ての軸の方向を決める必要がありますが、XY座標だけを取り扱う2次元の場合は、Z軸に相当する軸の方向は常に手前側に固定されていると考えることができるので、X軸とY軸の方向だけを解決すればOKです。

XYZ軸の回転イメージ(X→X'、Y→Y'、Z→Z')

手法

1ボーンIKにはいくつかの手法がありますが、ここでは三角比を使ってヨー回転量とピッチ回転量を計算する手法を紹介します。

前提知識2：ヨー回転・ピッチ回転について

その前に、ヨー回転、ピッチ回転について簡単に説明しておきます。

  • ヨー回転というのは進行方向に対して垂直上方向を回転軸とする回転です。
    進行方向基準で姿勢の左右方向を規定します。
  • ピッチ回転というのは進行方向に対して水平左方向を回転軸とする回転です。
    進行方向基準で姿勢の上下方向を規定します。

この他にロール回転というのもあって、これは進行方向軸を回転軸とし、進行方向基準で姿勢の捻じれ具合を規定しますが、ここでは一旦無視します。※あとでまた登場します。

ここでは、ヨー回転軸をZ軸、ピッチ回転軸をY軸にとり、ヨー回転角をθz、ピッチ回転角をθyとして説明します。*2

ヨー回転とピッチ回転

ヨー回転軸がZ軸なのでヨー回転ではX軸とY軸だけを回転し、ピッチ回転軸がY軸なのでピッチ回転ではX軸とZ軸だけを回転します。必然的にロール回転軸はX軸となり、ロール回転ではY軸とZ軸だけを回転します。

1ボーンIK手順
  1. IKの目標位置を関節のローカル座標に変換する
  2. ローカル座標から三角比を用いてcosθz, sinθz, cosθy, sinθyを計算する
    • \displaystyle{ \cos{θ_z} = x / \sqrt{x^2 + y^2} }
    • \displaystyle{ \sin{θ_z} = y / \sqrt{x^2 + y^2} }
    • \displaystyle{ \cos{θ_y} = \sqrt{x^2 + y^2} / \sqrt{x^2 + y^2 + z^2} }
    • \displaystyle{ \sin{θ_y} = z / \sqrt{x^2 + y^2 + z^2} }
  3. 関節の姿勢をcosθz, sinθzでヨー軸回転、cosθy, sinθyでピッチ軸回転する *3

ヨー回転(Z軸)+ピッチ回転(Y軸)時の三角比

赤いライン(X軸)に沿っている灰色表示の骨がIK適用前の初期配置です。
そこからIK目標位置(白青のチェッカーマーク中心)の方向に向けてヨー軸(Z軸)回転させた状態が中央の灰色表示の骨となり、更にそこから目標位置の方向にピッチ軸(Y軸)回転させた最終状態が水色表示の骨となります。

三角比の計算は、上の図を参考にしてください。
いきなり三角関数が出てきましたが、cos=底辺 / 斜辺、sin=高さ / 斜辺なので、手順2.のような式になります。
斜辺は三平方の定理 *4 で求めます。

この手法は3次元での1ボーンIKの一例ですが、ピッチ軸回転を無視することで、そのまま2次元でのIKにも使えるのが利点です。

その他の手法もざっくり紹介

1ボーンIKは他にも外積を用いる手法や、クォータニオンを用いる手法があるので、簡単に概要を紹介しておきます。

外積を用いる手法は回転を用いずにXYZ各軸を生成する手法ですが、今回説明したヨー回転＋ピッチ回転による手法と実質的に同じ結果が得られます。

クォータニオンを用いる手法は、元の進行方向ベクトルと目標位置までの方向ベクトルから計算できる内積と外積の結果を利用してクォータニオンを生成し、このクォータニオンで姿勢を回転させる手法です。ヨー＋ピッチ回転方式とは、進行方向となるX軸の方向は一致しますが、Y軸とZ軸の方向が異なる結果となります。

Up Vector Constraint

ヨー回転とピッチ回転の組み合わせで、目標位置の方向に関節の進行方向を向ける1ボーンIK手法を紹介しましたが、このままではロール回転については全く制御されていない状態です。*5

Up Vector Constraint(アップ・ベクター・コンストレイント=上方ベクトル拘束)は、関節のロール回転軸に対して垂直な任意の軸を上方ベクトルとして設定し、この上方ベクトルが拘束用の目標位置を向くようにロール回転軸の回転量を拘束する手法です。これはロール回転を制御する1ボーンIKだとも言えます。

Z軸に対するUp Vector Constraint(赤い矢印がロール回転、白赤チェッカーの中心が拘束用目標位置)

上方ベクトルはロール回転軸=X軸に垂直ならばどのような方向でも構いませんが、一般的にはY軸やZ軸、あるいはそれらの負方向を設定することが多いと思うので、ここではそれを前提に手順を紹介します。
以下の手順は、1ボーンIKを適用した後の追加処理となります。

Up Vector Constraintの手順
  1. 拘束用の目標位置 *6 を関節のローカル座標に変換する
  2. ローカル座標から三角比を用いてcosX, sinXを計算する
    • \displaystyle{ \cos{X} = y / \sqrt{y^2 + z^2} }
    • \displaystyle{ \sin{X} = z / \sqrt{y^2 + z^2} }
  3. Up Vectorとして選択する軸の種類によってcosX, sinXを変換する
    • Y軸：変更しない *7
    • Z軸：cosX = sinX, sinX = - cosX
    • 各軸の負方向合わせの場合は、上記手順で求めたcosX, sinX両方を符号反転する
  4. cosX, sinXで関節をロール回転する

1ボーンIK本体の方で三角比を用いたヨー回転＋ピッチ回転の手法で説明したので、こちらも三角比で計算する手法を紹介しましたが、クォータニオンを用いて計算する方法もあります。

2ボーンIK

概要

2ボーンIKとは、連結された2本の骨の先端位置が与えられた目標位置に到達するように、2本それぞれの骨の姿勢を同時に決定するIK処理です。
人間の手足の構造に適用するのに非常に適しているため、Limb IK(リム=肢)と呼ばれることも多いです。

2ボーンIKはその基本アルゴリズムだけで、2本目の骨の関節の回転軸が1軸に限定されることや、その回転方向を1方向に限定できることがメリットです。 *8

手法

こちらもいくつかの手法が知られていますが、余弦定理を用いる手法が一般的です。骨が増えた分だけ少し複雑になるので理論背景を交えつつ順番に説明します。

理論背景を交えた手順説明

まずは前項で説明した1ボーンIKを用いて第1関節を目標位置の方向に向けます。*9

第1関節の方向を1ボーンIKを用いて目標位置の方向に向ける

目標位置に向けた第1関節の進行方向軸を基準として、第2関節の回転軸を法線とする平面を想定します。この図では手前側に法線が向いた状態となっています。
第1関節も第2関節もこの法線方向を回転軸とした1軸回転を行うため、ここからは2次元での問題として扱います。
この平面上で、第2関節の先端が目標位置に到達するように、2本の関節を回転させて以下のような三角形を形成した状態を想定します。

平面上に2本の骨が構成する三角形を想定した図

辺a、辺bの長さは、それぞれ1本目と2本目の骨の長さに相当します。これは事前に分かっている既知の値です。また、辺cの長さは1本目の関節の位置と目標位置との距離に相当しており、これは2点間の距離を計算することで求まります。このように三角形の3辺の長さが既知なので、余弦定理を用いてcosB, cosCを求めることができます。

  • \displaystyle{ \cos{B} = \bigl(c^2 + a^2 - b^2\bigr) / 2ca }
  • \displaystyle{ \cos{C} = \bigl(a^2 + b^2 - c^2\bigr) / 2ab }

cosが決まれば \displaystyle{ \cos^2{θ} + \sin^2{θ} = 1 } の関係からsinも計算できます。

  • \displaystyle{ \sin{B} = ±\sqrt{1 - \cos^2{B}} }
  • \displaystyle{ \sin{C} = ±\sqrt{1 - \cos^2{C}} }

sinの符号は回転方向の符号と一致するため、ここでの決定は一旦保留して、回転方向がどうなっているのかを確認する必要があります。各関節の回転方向を表した図を以下に示してみました。

各関節の回転方向を示した図

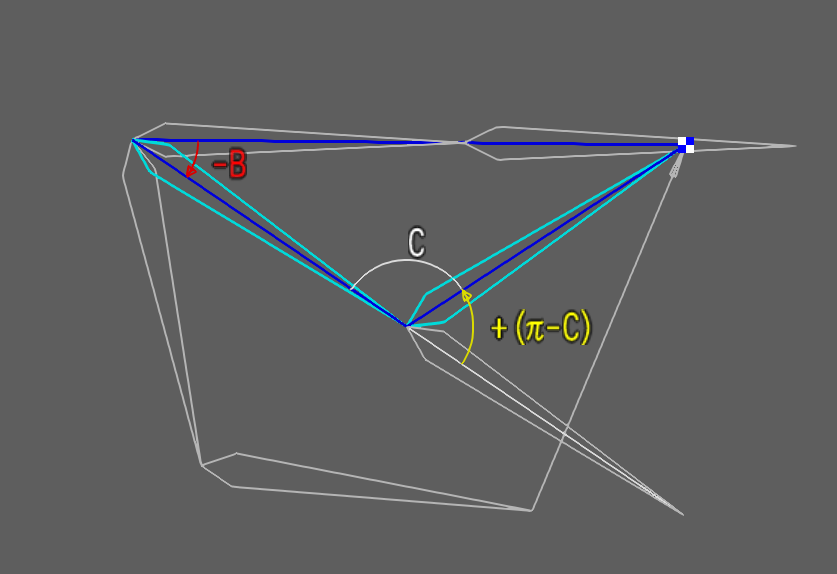
回転方向について考える前に、第2関節の回転角が余弦定理で求めた三角形abcの内角Cではなく、実際には外角のπ-Cとなっている点について考慮しなければなりません。
といっても、ここは以下の公式にしたがってcosCの符号を反転するだけで構いません。sinCの値はそのままです。

  • \displaystyle{ \cos{(π-C)} = -\cos{C} }
  • \displaystyle{ \sin{(π-C)} = \sin{C} }

改めて回転方向について話を戻します。
回転方向が反時計回りの場合は正方向の回転で、時計回りの場合は負方向の回転となります。この図によると、第1関節の回転Bは負方向への回転で、第2関節の回転π-Cは正方向の回転ということになります。
回転方向の正負はsinθの正負だけで表現できるので、cosの符号は変化しません。
回転方向を考慮した最終的なcosとsinの組み合わせは以下のようになります。

  • 第1関節：\displaystyle{ \cos{B} }, \displaystyle{ -\sin{B} }
  • 第2関節：\displaystyle{ -\cos{C} }, \displaystyle{ \sin{C} }

それぞれの関節についてcosとsinが決まったので、これらを使った回転変換で姿勢を作ることができるようになりましたが、2ボーンIKとしてはまだ考慮しなければならないことがあります。

2ボーンIKの条件を満たす三角形は、辺cの反対側にも想定することができるからです。

回転方向が反対となる逆側の三角形

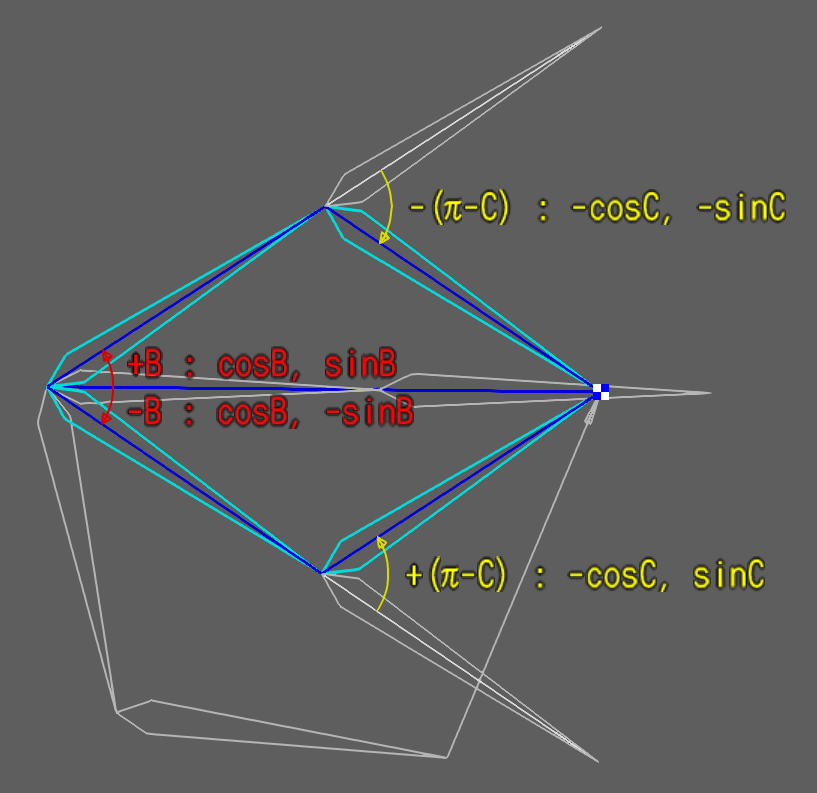
もう1つの三角形はBとCの回転方向を正負逆にしたものなので、既に求めているsin値の符号変換だけで対応可能です。

  • 第1関節：\displaystyle{ \cos{B} }, \displaystyle{ \sin{B} }
  • 第2関節：\displaystyle{ -\cos{C} }, \displaystyle{ -\sin{C} }

2ボーンIKの計算をする場合に、どちらの三角形による結果を選択するのかは、第2関節の回転方向が正負どちらであるかという基準で決定することが一般的です。これらはあらかじめどちらか一方に決めたものを選択することもあれば、両方に回転可能な場合も考慮して、IKを適用する前にどちら側に関節が曲がっていたかを調べて、同じ方向に曲がるような選択をする場合もあります。*10　いずれにせよ、第2関節の回転方向が正なら下の三角形、負なら上の三角形を選択します。余弦定理で求めるcosの結果は一緒なので、単純にsinの符号の組み合わせの選択を行います。

回転方向の設定について

第2関節の回転軸がどの軸になるかや、回転方向が正負どちらになるのかについては、2ボーンIKを適用する対象の構造に依存します。したがって、回転軸や回転方向を規定する設定項目を用意しておくのが良いでしょう。

人体モデルに適用する場合、一般的な作り方だと腕に設定する場合と足に設定する場合では、回転方向は逆になることが多いようです。当てはめてみて逆に曲がってしまったらもう一方の設定にすれば良いだけなので、そんなに難しく考える必要はありません。

2ボーンIKの手順(まとめ)
  1. 1ボーンIKを用いて目標位置の方向に第1関節を向ける
  2. 余弦定理でcosB, cosCを求める(cosCは符号反転する)
  3. sinB, sinCを求める(符号は正とする)
  4. 第2関節の回転方向設定によりsinB, sinCいずれかの符号反転を行う
    • 正回転：-sinB
    • 負回転：-sinC
  5. 得られたcos, sinの組み合わせで、各関節を回転させる

 

次項以降では、2ボーンIKに対するいくつかの基本的な機能拡張について説明します。

Up Vector Constraint

2ボーンIKは、1ボーンIK適用後に第2関節の回転軸を法線とする平面上での三角形を想定して計算するという基本アルゴリズムでした。2次元の場合はこれ以上のIK解は存在しませんが、3次元の場合はロール軸回転が存在するため、無限の解が存在することになります。これらの中から任意の平面上の三角形を選択したい場合は、1ボーンIKの計算後にUp Vector Constraintをかけることで対応します。 *11

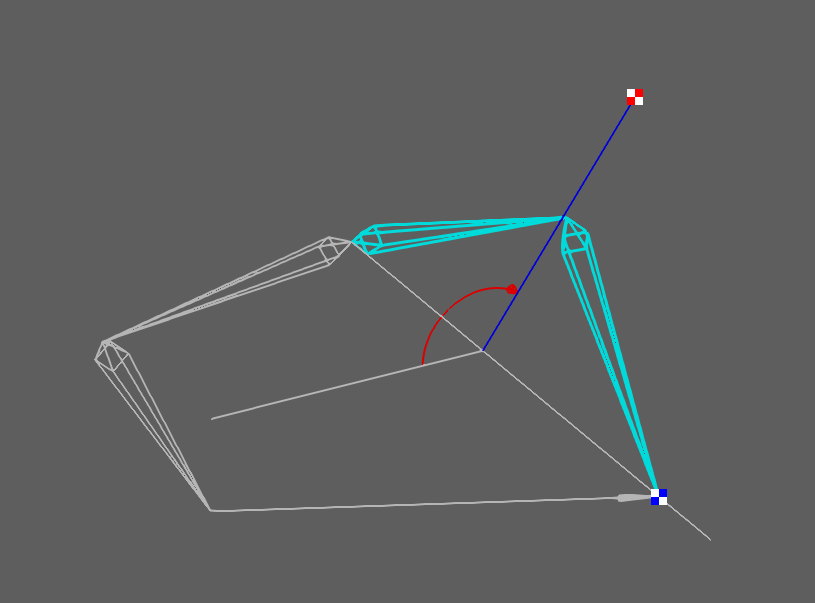
2ボーンIKへのUp Vector Constraint適用イメージ

キャラクターモーションの補正目的で2ボーンIKを使う場合は、元のモーション姿勢から1ボーンIKを適用した状態での平面をそのまま使い、Up Vector Constraintをかけないことも多いですが、そこから手足の開き具合の調節が必要な場合などには、この機能に頼らなければなりません。

第2関節の回転角制限

2ボーンIKでは第2関節の曲がる方向を選択することで、回転角の範囲が自動的に0～180°か-180～0°のいずれかに制限されますが、この曲がり具合の範囲を更に制限することができるので、その手法について説明します。

理論背景を交えた手順説明

通常の2ボーンIK処理の工程で、cの長さを目標位置と第1関節の位置との距離として求めますが、ここでも余弦定理を使うことで角Cの角度制限の問題を、辺cの長さの範囲制限の問題に落とし込み、第2関節の回転角制限を実現します。

ここでは実際の回転計算で考慮する三角形の外角(π-C)ではなく、余弦定理で求める対象となる三角形の内角Cの方で考えます。

角Cの最小回転角をθmin、最大回転角をθmaxとします。(0 ≦ θmin ≦ θmax ≦180°)
設定は角度で与えておいたとしても、実際には事前処理でcosθmin, cosθmaxを求めておくのが効率的です。
辺a、辺bの長さと、それらがなす角Cに対するcosθmin, cosθmaxが既知なので、余弦定理で辺cの長さの最小値と最大値が決まります。 *12

  • \displaystyle{ c_{min} = \sqrt{ a^2 + b^2 - 2ab \cos{θ_{min}}} }
  • \displaystyle{ c_{max} = \sqrt{ a^2 + b^2 - 2ab \cos{θ_{max}}} }

実際の距離から求めた辺cの長さを、この\displaystyle{ c_{min} }と\displaystyle{ c_{max} }で範囲制限した結果を新たなcとして2ボーンIKを計算することで、第2関節の角度が範囲制限された状態で、対応する第1関節の角度と共に求まります。

第2関節の角度制限適用例(最小角度：30°、最大角度：170°)

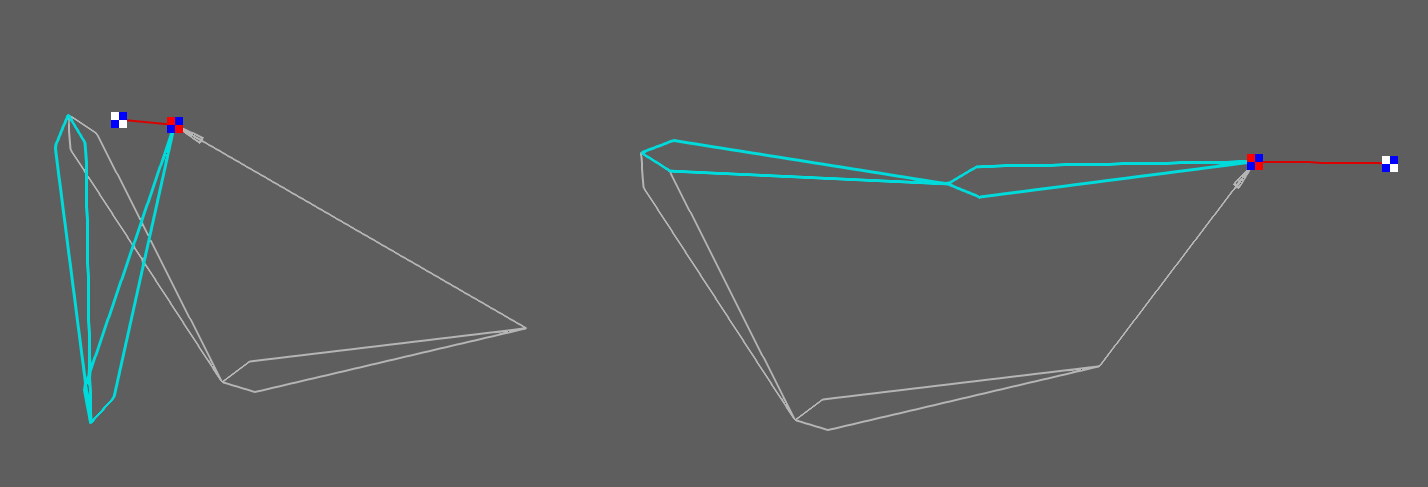
最初からcの長さを規定するパラメーター(距離に対する比率など)で範囲制限することもありますが、その方法だとaとbの長さの比率がキャラによって異なる場合に、制限する角度を一定に保つことができないという問題があります。aとbの長さの比率が固定なら\displaystyle{ c_{min} }と\displaystyle{ c_{max} }は完全に事前計算可能なので、この方式を選択することにより2ボーンIKの処理負荷が余計に増えることはありません。

回転角制限の副作用

回転制限がかかると目標位置への到達という、IKが達成すべき本来の目的が達成できなくなってしまいます。しかしながら、目標位置への到達が多少阻害されたとしても、挙動の乱れや関節間の回転限界を超えた不自然な姿勢を見せないことの方が重視されるケースも多々あるため、そうしたメリット・デメリットを天秤にかけて、必要な場合には回転角制限をかけることを選択しなければなりません。

回転角制限が必要となる事例

2ボーンIKを適用する事例では、実はそこまで回転角制限が必要になるケースはありません。これは2ボーンIK自体に最初から関節が逆側に曲がらないような回転制限が自動的にかかっているためで、これは2ボーンIKの大きなメリットと言えます。
ただ、目標位置の配置によっては2本の関節が伸びきったり曲がったりするような状態、すなわち第2関節の最大角度が180°まで振り切ったり少し戻ったりするようなギリギリの状態になることがあり、そのような状態では目標位置の僅かな移動量に対し角度の変化量が極端に大きくなることから、その急激な挙動変化が不自然な動きとして目立つようになります。このような急激な角度変化の影響を緩和し目立たなくする目的で、最大角度を180°よりも少し小さい値 *13 に設定することで関節が完全に伸びきらないように設定しておくことがあります。手足を限界まで伸ばさなくても支障がない、あるいは限界まで伸び切って欲しくない場面ではメリットしかないので試してみてください。

2ボーンIKをキャラクターに適用する

エンドエフェクターについて

2ボーンIKを人型キャラクターなどに適用する場合は、腕や足に設定することが多いですが、実際に当てはめてみると腕部だと上腕＋前腕、脚部だと腿＋脛という割り当てになり、手足や足先の関節が対象から外れてしまうので、1ボーン分足りないと感じるかもしれません。実際のゲーム中で位置や姿勢を合わせたいのは手の指先や足先だったり足の裏面だったりするのに、このままではIK処理が合わせるのは手首、足首の位置になってしまうからです。

2ボーンIKの人型キャラクターへの適用例

IKの位置や姿勢を目標に合わせたい部位のことをエンドエフェクター、あるいは単にエフェクターと呼びます。これは末端効果器という意味で、IKを使って動作させるロボットアームなどの先端に接続されて実際に作業を行う装置を想定していることから、このような呼び方をしています。

先程の人型キャラクターの例に話を戻すと、手先や足先の部位がエフェクターに相当することになりますが、このエフェクター部位はIKの計算対象には含まなくて良いのです。
あらかじめ何らかの手法で求められているエフェクターの姿勢や位置から逆算して、途中の関節の姿勢や位置を計算するのがIKなので、エフェクターの位置を目標位置として渡してしまえば、IK内ではエフェクターそのものの制御をする必要がないからです。*14

エフェクターの目標位置の置き換え

もう少し具体的に説明すると、もしエフェクターの姿勢があらかじめ固定されているのなら、実際にエフェクターが効果を作用させたい位置とエフェクターの関節位置との相対的な位置関係も固定されていることになります。であれば本来の目標位置から、この相対的な位置差分を引いた位置をIKの目標位置にすれば、エフェクターが作用する位置にも自動的に合うことになります

人体で例えれば、手先エフェクターの実際の作用点が指先だった場合は、その時点での指先の位置と手先エフェクターの関節位置との相対的な位置関係を求めておけば良いのです。

エフェクターの作用位置を考慮した目標位置の平行移動

図で説明すると、エフェクターの先端部を本来の目標位置である白のチェッカーマーク位置に合わせたい場合に、エフェクターの位置差分を考慮して得られたピンクのチェッカーマーク位置を2ボーンIKの目標位置として計算することで、エフェクターの先端位置は自動的に白のチェッカーマークに到達するという仕掛けです。

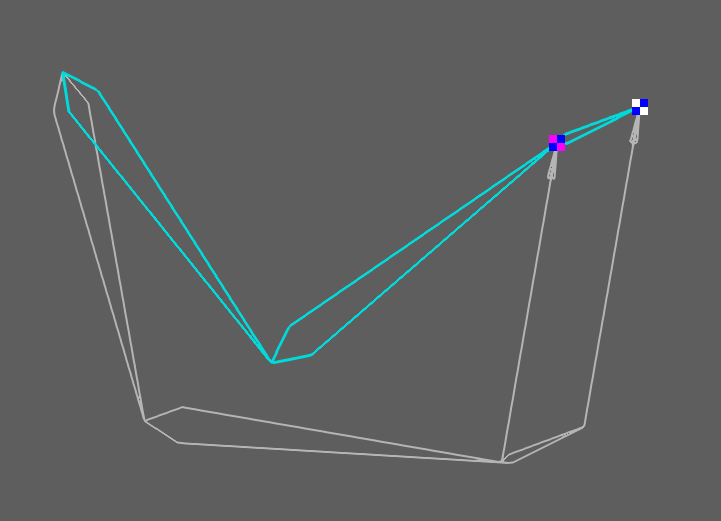
エフェクターの関節位置が目標に到達すると実際の作用位置も自動的に目標に到達する

この手法は多くのIKに応用可能で、IK制御が必要な連鎖数を1つ減らすことが可能となります。*15

2ボーンIK＋エフェクター部位の制御イメージ

疑似3ボーンIK

エフェクターの姿勢が固定されたままだと、IKによる姿勢変化が大きくなった時に、親となる第2関節とエフェクターとの間の回転角が極端な状態になることがあります。

エフェクター部位の関節の角度が極端になった例(左手)

エフェクターの固定姿勢を決める際に、目標位置や対象の状態を見てある程度の変化を付けておいたり、目標位置への到達を多少犠牲にしてでも回転制限の範囲内になるようにエフェクターの姿勢を後から変更する方法も考えられますが、どうせならエフェクター部位もIKに計算させてしまいたいと考えるはずです。

エフェクターもIKに含めて解決した場合

人間の手足のケースならば3ボーンに対応したIKを適用することで解決できそうですが、ここでは2ボーンIKを使って疑似的に3ボーン分のIK処理を実現する手法について紹介します。

疑似3ボーンIKの手順
  1. IK適用前の第2関節と第3関節間のローカル回転差分を計算する
  2. 第3関節の関節位置と先端位置の移動差分を計算する
  3. 手順2.で求めた移動差分を目標位置から差し引いた位置を新たな目標位置とする
  4. 第1関節と第2関節に2ボーンIKを適用する
  5. 手順1.で求めたローカル回転差分を用いて、第3関節の姿勢を再構成

  6. 手順5.で求めた第3関節の姿勢と、第3関節の初期姿勢の中間姿勢を計算し、これを第3関節の姿勢とする
    • 中間姿勢のブレンド率は追加パラメーターとして別途与える必要がある
    • 0%だとブレンドターゲット側、100%だと初期姿勢側としてブレンドする
  7. 手順6.のブレンド率が100%以外(未満)の場合は、手順2.～4.を再び実行する *16

 

細かく手順を書きましたが、ざっくり言うと、2ボーンIK計算後に第3関節の姿勢を初期姿勢を使って加工し、目標位置からずれた分を再度2ボーンIKを計算することで解消しています。手順2.～4.は、2ボーンIKで必要となる手順そのものなので、そのまま機能を呼び出せばOKです。

ブレンド率の調整で出る結果の幅のサンプルが以下の画像となりますが、この幅は第3関節の初期姿勢だけでなく目標位置の場所によっても広がったり狭まったりします。

ブレンド率による結果の幅

人型キャラクターに適用する時の様にエフェクター部位を第3関節とする場合には、必要なら姿勢を外部から与えて拘束してもいいのですが、通常は元のモーションで得られるFK姿勢をそのまま使えば十分です。下の適用例は疑似3ボーンIKとUp Vector Constraintのみで、Tポーズの状態から1分くらいで適当にポーズ付けしたものです。

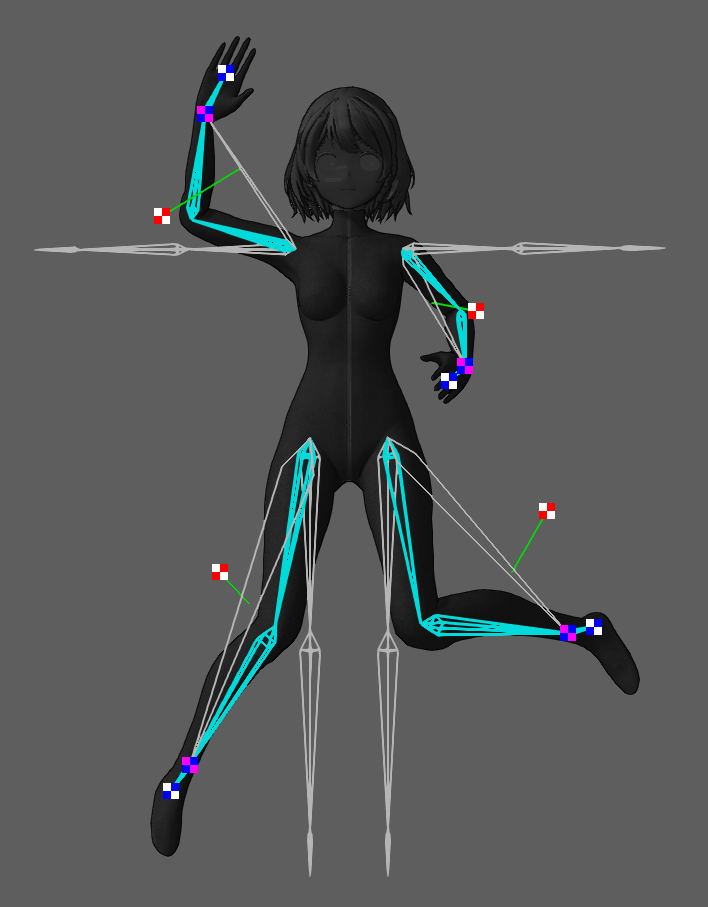
疑似3ボーンIK(+Up Vector Constraint)の人型キャラクターへの適用例
別バージョン

上の説明では回転差分を用いることで元のFK姿勢とのブレンドを行う方式について説明しましたが、回転差分を用いずに第2関節と同じ姿勢をそのままブレンド対象とするやり方もあるので、設定によって使い分けられるようにしておくと便利です。

他にも2ボーンIKの適用後にエフェクター部位の回転制限をかけて目標位置からずれてしまった結果に対して、追加処理で手順2.～4.を適用することで、回転制限もある程度考慮しつつ目標位置に到達するといった簡易方式も考えられます。 *17

特徴

追加で第3関節のブレンド率の設定が必要となることや、2ボーンIKを2回計算することによる処理負荷増の問題はありますが、2ボーンIKの仕組みやメリットを生かしたまま3ボーン分のIK処理が実現できるという点で、導入し易いのではないかと思います。特にエフェクターの先端は目標位置に到達して欲しいけど、姿勢拘束はボチボチで良いという場合に最適です。

また、一般的に四足歩行動物の四肢の制御は人間の手足よりも1ボーン多い関節制御が必要となるため、3ボーン以上に対応したIKアルゴリズム＋エフェクター部位の制御を行う必要がありますが、この手法を用いることで2ボーンIKの機能しかなくても四足歩行動物の四肢の制御への対応が可能となります。以下は動作サンプルです。

疑似3ボーンIK＋エフェクター制御の動作サンプル(前足→後ろ足→ブレンド率制御の様子)

まとめ

IKの基本的な概念、基本処理となる1ボーンIKと今でも広範囲で使われている2ボーンIKの具体的な処理内容について説明しました。数学の授業で習った時には何に使うのか今ひとつピンと来なかった余弦定理も、ここではしっかり役に立っています。

IKアルゴリズムには他にも様々な手法があり、それぞれ適用できる範囲や得意分野が異なります。また今でも新しいIKアルゴリズムや既存のアルゴリズムの改善の提案が各所で発表されているので、そうした手法についても学ぶきっかけになればと思います。

特に昨今は商用ゲームエンジンに標準機能として様々なIK処理が実装されるようになったので、自分でIK処理を新たに作成する機会は減っているかも知れません。それでも自社エンジンやタイトルにIK処理を組み込む事例はまだまだありますし、仮に既に用意されているIKの機能を使うだけであっても、その仕組みや特徴を理解しているのとそうでないのとでは、同じIK機能を使ってるにも関わらずゲーム上での挙動が大きく変わることがあったりするので、IK処理の知識は無駄になりません。

今回はIK本体のアルゴリズムを中心に解説しましたが、実際のゲーム制作においては、IKに与える目標位置の取得方法や加工の仕方、各種パラメーターの設定にも工夫が必要となり、最終的な挙動に与える影響度としてはむしろそちらの方が重要だったりもします。今後機会があれば、そういった内容にも触れられれば良いなと思っています。

終わりに

セガでは商用ゲームエンジンだけでなく自社開発エンジンによるゲーム開発も行われており、開発メンバーとして一緒に働ける仲間を幅広く募集しています。セガでのゲーム開発に興味がある方は、下記サイトにアクセスしてみてください。

recruit.sega.jp

©SEGA

 

*1:＋α

*2:この場合は必然的にX軸がロール回転軸となります。

*3:回転の処理はX軸、Y軸、Z軸それぞれに対して計算する必要があります。1つずつ計算しても良いのですが、通常は行列などを使ってまとめて処理します。

*4:中学3年で習う「底辺の2乗+高さの2乗=斜辺の2乗」です。

*5:これは外積版やクォータニオン版も同様です

*6:1ボーンIK用の目標位置とは別に設定される

*7:手順2.で求めたcosX, sinXの式はY軸合せの場合の式なので

*8:これは他のIKだと非常に面倒な追加処理を要求されます

*9:この図では第2関節も一緒に追従させていますが、計算上は第2関節は放置していて問題ありません。

*10:適用前の角度が180°の場合は方向が決められないので、その場合に正負どちらを優先するかは決めておく必要があります。

*11:この処理自体は1ボーンIKにかかるものなので計算手順も同じです。

*12:余弦定理の式が先程とは違いますが、cについて展開し直しただけです

*13:例えば170～175°程度

*14: IKで決定した最終位置にエフェクター部位を接続する処理も、IK処理全体の枠組みの中には含まれますが、IKアルゴリズムそのものが解決する内容ではないという意味です。

*15:エフェクター部位の情報もIK計算に必要な場合は残す必要があります

*16:100%の場合は、そのままIK処理を終了する

*17:その場合、結果として回転制限を突破する可能性もあります

Powered by はてなブログ